❯ Tree traversal
트리의 모든 노드를 한번씩 방문하는 것을 트리 순회라고 한다.
트리 구조는 계층적 구조를 가지므로 모든 노드를 순회하는 방법으로는 크게 세가지가 있다.
전위 순회(Preorder traverse)
먼저 노드를 방문하고, 왼쪽 서브트리를 전위순회하고, 오른쪽 서브트리를 전위순회 하는것을 말한다.
트리구조에서 방문하는 순서는 아래와 같다.

<코드 예시>
/* 최소한의 기능만 구현되어 있습니다.
자식 노드가 없는 경우는 node == null이라고 가정합니다.
이미 이진 트리는 구현되어 있다고 가정합니다. */
class Node {
String data;
Node left;
Node right;
public Node getLeft() {
return left;
}
public String getData() {
return data;
}
public Node getRight() {
return right;
}
}
public ArrayList<String> preOrder(Node node, ArrayList<String> list) {
if (node != null) {
list.add(node.getData());
list = preOrder(node.getLeft(), list);
list = preOrder(node.getRight(), list);
}
return list;
}
탐색 종료 시 list의 값 -> ["A", "B", "D", "H", "I", "E", "J", "K", "C", "F", "L", "M", "G", "N", "O"]중위 순회(Inorder traverse)
왼쪽 서브트리를 중위 순회하고, 노드를 방문하고 오른쪽 서브트리를 중위순회하는 방식을 말한다.
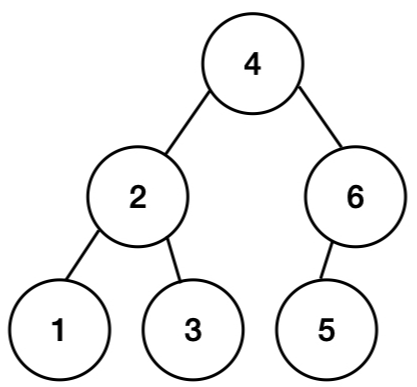
<코드 예시>
/* 최소한의 기능만 구현되어 있습니다.
자식 노드가 없는 경우는 node == null이라고 가정합니다.
이미 이진 트리는 구현되어 있다고 가정합니다. */
class Node {
String data;
Node left;
Node right;
public Node getLeft() {
return left;
}
public String getData() {
return data;
}
public Node getRight() {
return right;
}
}
public ArrayList<String> inOrder(Node node, ArrayList<String> list) {
if (node != null) {
list = inOrder(node.getLeft(), list);
list.add(node.getData());
list = inOrder(node.getRight(), list);
}
return list;
}
탐색 종료 시 list의 값 -> ["H", "D", "I", "B", "E", "J", "K", "A", "L", "F", "M", "C", "N", "G", "O"]후위 순회(Postorder traverse)
왼쪽 서브트리를 후위 순회 하고, 오른쪽 서브트리를 후위 순회 하고, 노드를 방문하는 방식을 말한다.

<코드 예시>
/* 최소한의 기능만 구현되어 있습니다.
자식 노드가 없는 경우는 node == null이라고 가정합니다.
이미 이진 트리는 구현되어 있다고 가정합니다. */
class Node {
String data;
Node left;
Node right;
public Node getLeft() {
return left;
}
public String getData() {
return data;
}
public Node getRight() {
return right;
}
}
public ArrayList<String> postOrder(Node node, ArrayList<String> list) {
if (node != null) {
list = postOrder(node.getLeft(), list);
list = postOrder(node.getRight(), list);
list.add(node.getData());
}
return list;
}
탐색 종료 시 list의 값 -> ["H", "I", "D", "J", "K", "E", "B", "L", "M", "F", "N", "O", "G", "C", "A"]
❯ 그래프의 탐색
위에서 본 트리 순회와 같이, 그래프를 순환하는 방식은 크게 두가지로 나뉜다.
BFS(Breadth First Search)
너비 우선 탐색. 말 그대로 같은 레벨(너비)을 먼저 탐색하는 방법을 말한다.
즉 시작 정점에 인접한 모든 정점을 우선 방문하여 탐색하는 방법이다.
최단거리를 구해야할 경우 유리하며, 검색 규모가 크지 않고 검색 시작으로부터 원하는 대상이 멀지 않을 경우 유리하다.
- 장점 : 두 정점 사이에 최단 경로를 찾을 수 있다.
- 단점 : 경로가 매우 길면 많은 기억공간을 필요로 한다.

<코드 예시>
Queue를 활용하여 구현된다. FIFO 방식으로 동작하며, 시작 노드를 큐에 삽입한 후 인접한 노드를 뷰에 순차적으로 삽입하며 탐색을 진행한다.
- BFS는 큐(Queue) 자료 구조를 활용하여 구현됩니다.
- 시작 노드를 큐에 삽입한 후, 큐가 빌 때까지 반복을 시작합니다.
- 큐에서 현재 정점을 가져옵니다. (queue.poll() 활용)
- 현재 정점은 이미 이동했다고 방문 여부를 체크합니다. ex) visitied[index] = true;
- poll()을 활용해 가져온 정점을 기준으로, 인접한 정점을 모두 큐에 삽입합니다.(queue.offer() 활용)
- 다시 반복으로 돌아와서, 큐가 빌 때까지 인접한 정점을 모두 큐에 삽입하며 그래프를 끝까지 순회합니다.
/**
* BFS 인접행렬 : 너비 우선 탐색을 구현한 템플릿 예제입니다.
*
* @param array : 각 정점을 행/열로 하고, 연결된 정점은 1로, 연결되지 않은 정점은 0으로 표기하는 2차원 배열
* @param visited : 방문여부 확인을 위한 배열
* @param src : 방문할 정점
* @param result : 방문했던 정점 리스트를 저장한 List
*
**/
public ArrayList<Integer> bfs_array(int[][] array, boolean[] visited, int src, ArrayList<Integer> result) {
//bfs의 경우 큐를 사용합니다.
Queue<Integer> queue = new LinkedList<>();
//시작 지점을 큐에 넣어주고, 해당 버택스의 방문 여부를 변경합니다.
queue.offer(src);
visited[src] = true;
//큐에 더이상 방문할 요소가 없을 경우까지 반복합니다.
while (!queue.isEmpty()) {
//현재 위치를 큐에서 꺼낸 후
int cur = queue.poll();
// 현재 방문한 정점을 result에 삽입합니다.
result.add(cur);
//전체 배열에서 현재 버택스의 행만 확인합니다.
for (int i = 0; i < array[cur].length; i++) {
//길이 존재하고, 아직 방문하지 않았을 경우
if(array[cur][i] == 1 && !visited[i]) {
//큐에 해당 버택스의 위치를 넣어준 이후
queue.offer(i);
//방문 여부를 체크합니다.
visited[i] = true;
}
}
}
//이어진 모든 길을 순회한 후 방문 여부가 담긴 ArrayList를 반환합니다.
return result;
}DFS(Depth First Search)
깊이 우선 탐색. 한 정점에서 시작해서 다음 경로로 넘어가기 전에 해당 경로를 완벽히 탐색하는것을 의미한다.
경로의 특징을 지정해야하거나(ex. 경로에 같은 숫자가 있으면 안된다) 미로 생성과 같은 문제, 검색 대상 그래프가 큰 경우 유리하다.
- 장점 : 목표 노드가 깊게 있으면 해를 빨리 찾을 수 있다.
현 경로상의 노드만 기억하면 되므로 저장 공간 수요가 적다. - 단점 : 해가 없는 경로에 깊이 빠질 수 있다.
구해진 해가 최단 경로라는 보장이 없다.

깊이제한 : 탐색 과정이 시작 노드에서 한없이 진행되는 것을 막기 위해 사용하는 방법.
백트래킹 : 깊이 제한에 도달했는데도 목표 노드가 없다면 부모 노드로 되돌아오는것.
<코드 예시>
Stack 자료구조나 재귀를 통해 구현할 수 있다. (일반적으로 재귀를 통해 구현된다.)
- 스택(Stack) 자료 구조나 재귀를 통해 구현할 수 있습니다. 일반적으로 재귀를 통해 구현합니다.
- 방문했던 정점인지 확인합니다. 방문했다면 재귀 호출을 종료합니다.
- 단순 출력이 아닌, 방문 여부를 저장할 데이터가 필요하다면 해당 데이터에 방문 여부를 저장한 후, 저장한 데이터를 반환합니다.
- 방문하지 않았다면, 방문 여부를 체크합니다. ex) visitied[index] = true;
- 해당 정점에 연결된 모든 정점을 재귀호출로 순회합니다.
/**
* DFS 인접행렬 : 깊이 우선 탐색을 구현한 템플릿 예제입니다.
*
* @param array : 각 정점을 행/열로 하고, 연결된 정점은 1로, 연결되지 않은 정점은 0으로 표기하는 2차원 배열
* @param visited : 방문 여부 확인을 위한 배열
* @param src : 방문할 정점
* @param result : 방문했던 정점 리스트를 저장한 List
*
**/
public ArrayList<Integer> dfs(int[][] array, boolean[] visited, int src, ArrayList<Integer> result) {
// 이미 방문했다면
if (visited[src] == true) {
result.add(src); // 방문한 정점을 저장
return result; // 저장한 데이터를 반환하며, 재귀호출을 종료
}
// 아직 방문하지 않았다면
visited[src] = true; // 방문한 정점을 표기
// 현재 정점에서 이동할 수 있는 정점을 순회하며 재귀 호출
for (int index = 0; index < array.length; index++) {
if (array[src][index] == 1) {
// 재귀 호출을 통해, 방문 여부를 담은 데이터를 반환과 동시에 할당
result = dfs(array, visited, index, result);
}
}
return result;
}오늘까지 Section2의 1주차 수업이 진행되었다.
계속해서 문제를 푸는 방식으로 진행됐는데 구조를 이해하고 알고리즘을 작성하는게 정말 어려웠다.
문제를 보고 막막할때도 있었고, 벌써 이렇게 어려워서 앞으로 어떡하지 하는 순간도 있었다.
그래도 오늘 선배와의 시간을 통해서 지금 어려운건 당연한거고, 계속 반복하다보면 언젠가는 될거라는 말을 들으면서 조금은 위안이 됐다. 코딩을 제대로 시작한지 한달밖에 되지 않았으면서 능숙하게 할 수 있을거라고 기대하는게 오히려 오만한(?) 생각이라는 느낌도 든다.
내일부터는 코딩테스트 관련 수업이 진행되는데 다시 자신감을 가지고 참여할 수 있도록
오늘 저녁에는 이때까지 풀었던 문제들을 다시한번 쭉 풀어봐야겠다.
'부트캠프 개발일기 > Algorithm' 카테고리의 다른 글
| 27일차: 알고리즘(Greedy, Brute-Force, Binary Search) (0) | 2023.03.22 |
|---|---|
| 26일차: 알고리즘(Algorithm)과 시간복잡도(Time Complexity) (0) | 2023.03.21 |
| 24일차: 자료구조(Graph, Tree, BST) (0) | 2023.03.17 |
| 23일차: 자료구조 (Stack, Queue) (0) | 2023.03.16 |
| 22일차: JSON, 재귀함수 실습 (1) | 2023.03.15 |


